IBM Quantum/Qiskit in QM Part I: Single Spins

Introduction

Hopefully, this will be the first of a series of posts about incorporating quantum computing into an undergraduate quantum mechanics course. It was during the first week of classes two years ago when I discovered the IBM Quantum Experience, which allows anyone to access actual quantum devices on the IBM cloud for free. At that point, I did not have the bandwidth to do much more than fiddle around with the hardware in my limited free time and encourage a few students to try it out as part of their course projects. Now that I’ve had some time to prepare to teach the course again, I’m ready to actually integrate this incredible resource into the class. For the uninitiated (as I was very recently!), Qiskit is an open-source software development kit (SDK) that allows users to access cloud-based, IBM quantum hardware. I feel like this needs to be said again: you can access IBM’s quantum computers using a free Python-based SDK.

Some caveats to what follows: I’m teaching a mix of juniors and seniors who have had experience using Glowscript since their first physics course and experience using Jupyter notebooks since at least their sophomore-level modern physics course. Computation is an integral part of our curriculum, so it’s not as daunting to jump into using Qiskit as it would be if this were their first exposure to Python. Also, our program is somewhat unusual in that we have a lab section associated with each of the four core upper-level courses (QM, E&M, Classical Mechanics, Thermal Physics) instead of having a dedicated “advanced lab” course. That’s two hours each week on top of the four contact hours for “lecture” that can be used for computation. Probably two thirds of that time was devoted to computational endeavors the last time I taught this course, and I expect a similar amount of time being used for that this semester. It would be a lot harder to incorporate quantum computing without those “extra” two hours per week.

To conclude this preamble, I should also note that IBM has a Quantum Educators program. One potential roadblock to using this technology in an in-person class setting is that you are competing with pretty much everyone else in the world for time on these devices–turns out that a lot of people are interested in quantum computing! As part of the Educators program, you get access to hardware not available to the general public as well as the ability to reserve priority access on several devices. I highly recommend that anyone looking to use this technology in a course apply for the Educators program. For in-person (time-constrained) activities or demonstrations, the Quantum Educators Program has been a life saver.

Motivation

So why incorporate quantum computing into an otherwise fine acceptable course on quantum mechanics? For starters, this is an incredible opportunity for students to get experience with cutting-edge technology. Most physics majors will not pursue academic careers in physics. If there were ever a way to make quantum mechanics relevant to future software engineers and data scientists, this is it.

From a more academic point of view, quantum computers provide an easily accessible experimental component to highly abstract topics like spin, entanglement, and quantum time evolution. It’s certainly possible to probe such physics experimentally, but this generally entails expensive equipment. For free, students can perform legitimate experiments on state-of-the-art quantum hardware.

I should also mention that I’m fairly new at all of this. Anything I write about is a work in progress. Fortunately, it’s quite fun to explore this technology. If you’d like to follow along within a Jupyter notebook, you can download a notebook here. For ease of reading (but with a total lack of functionality), an HTML depiction of the notebook is located here. That Jupyter notebook is a sample of what students are given. This will all be organized on GitHub at some point.

The textbook for this course is employs a spin-first approach, so we are talking about the Stern-Gerlach experiment on the first day and using the excellent SPINS program to simulate various experimental setups. For example, we might attempt to predict the measured counts for the following arrangement of spin analyzers if N = 10^{4} initially unpolarized spins are emitted from the source:

Screenshot of SPINS program simulation of Stern-Gerlach experiment in which \hat{S}^{z} is measured twice while \hat{S}^{x} is only analyzed between the two successive measurements. Students also show that the (expected) final counts change dramatically if only the “spin up” sample from the middle analyzer is fed into the final measurement.

Now, I like this program a lot. It’s fairly easy to use, and it doesn’t require any programming. Even its quirks are charming. But when we get to entanglement and multi-particle states, students essentially have to write their own simulator in Python. The last time I taught this course, students built such a program in stages with the first step being to create a program that reproduced the kinds of results they found using SPINS. But that felt really contrived. Why reinvent the wheel in a clunkier way? Instead of dragging students through that tedious process again, we can just use IBM hardware to perform the experiment and analyze the actual data.

Students install Qiskit on their own laptops and set up their own IBMQ accounts, and this takes some a lot of time. In the end, most ended up just using the excellent IBM Quantum Lab to use Qiskit in IBM’s cloud-based Jupyter lab. So on the first day of using Qiskit, I just had students go through a tutorial that introduces the correspondence between “spins” and “qubits” and walks them through how one can “measure” the spin projection along a particular direction. It’s a bit of work for a pretty modest task. But this is a nice opportunity to spin (pun intended) the fairly abstract idea of quantum states from an experimental point of view.

The textbook assigns the ket \left|+\right\rangle to the state which gives a measurement of S^{z} = \frac{\hbar}{2} and \left|-\right\rangle to the state which returns -\frac{\hbar}{2}. These states map to the qubit states \left|0\right\rangle and \left|1\right\rangle, respectively. The course textbook’s notation is not congruent with the traditional quantum computing conventions, in which \left|\pm\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left(\left|0\right\rangle \pm \left|1\right\rangle\right). Sticking with textbook notation and using \left|\pm\right\rangle_{x} for those superposition states is a major sin for which I will pay at some point in the near future.

Our first quantum circuits

To get students to go through the basic processes with absolute minimum complexity, we start out with the following incredibly basic circuit:

All this does is to initialize a qubit in \left|0\right\rangle and then measure the state, writing the result to the classical register. Why do something so boring? Well, I think there’s already a lot happening. Students are already using quantum computers to simulate spins, we haven’t talked about gates, and it’s a quick payoff that allows students to actually run something (as simple as it is) on a simulator and on a real quantum machine. Furthermore, it serves to demonstrate that the standard of initialization of qubits is in the state \left|+\right\rangle. But probably most importantly, it shows students what a measurement looks like. Making a simple histogram out of the job results gives the following:

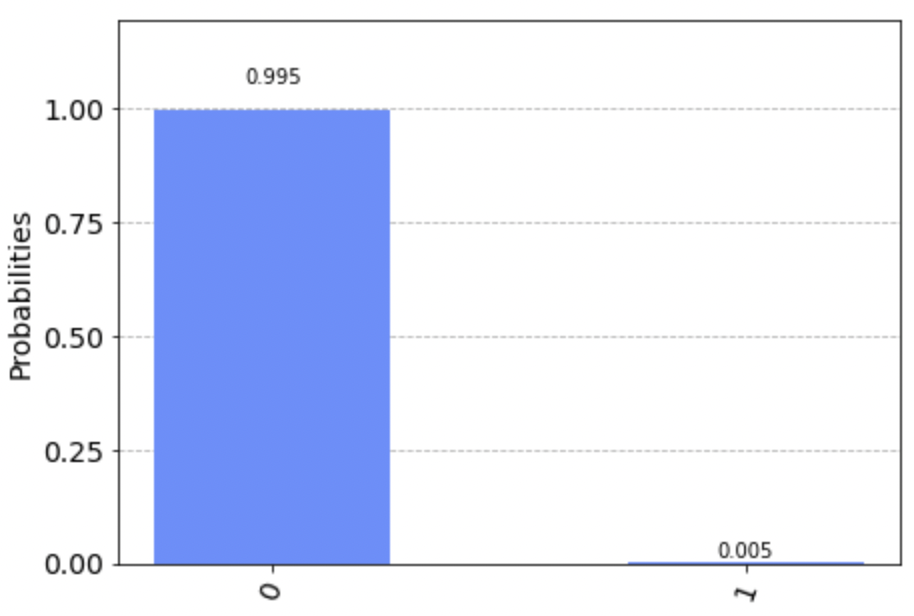
Result from real quantum hardware (ibmq_belem v1.0.18, one of the IBM Quantum Falcon Processors): most of the qubits are measured to be in the state ‘0’ corresponding to the spin state \left|+\right\rangle, while ‘1’ corresponds to \left|-\right\rangle.

A central idea in quantum mechanics is that the outcome of a particular measurement event is essentially unpredictable. The outcome is constrained to be one of the eigenvalues of the operator corresponding to this observable. The best we can do to predict outcomes is to work out a probability distribution. Experimentally, this only emerges after many measurements are made on identically prepared systems. Running a job actually consists of repeating a circuit many times with the default number of such “shots” set to 1024. Qiskit’s built-in histogram function turns the raw counts into a visual representation of the underlying probability distribution.

The other thing students can observe from this incredibly simple simulation is that present-day quantum computers are not error free. When they run this circuit on the simulator, the results show that the counts are entirely in the ‘0’ state. What else could happen? We just prepared a bunch of copies of the \left|0\right\rangle state and measured the state. But in the actual hardware, there are errors, and we only observe that most (>99\%) qubits are observed in the \left|0\right\rangle state. I don’t really plan on going into the advanced error mitigation procedures that have been developed, as we have enough going on already. For things that I plan on exploring in this course, the errors don’t appear to be large enough to pose much of a problem. Besides, students should get experience with imperfect data. And it actually paints a nice picture of the present state of the technology to show how these errors do tend to increase as more CNOT gates are used to simulate highly coherent multi-particle states. But that’s for later!

Introducing quantum computing in this course is motivated by the ability to simulate quantum mechanical systems. So what we do doesn’t really rely on the traditional background one builds up to study quantum computing (theory of computation, logic gates, and so on). Consequently, I’m introducing topics only as I need them, and so some of this might seem to arranged strangely. For example, the first gate we really use is a rotation gate. Why? Because we need it to measure spin projection about arbitrary axes.

What I really love about using these devices is that you have to think like an experimentalist. This does not come easy to me, but that also makes it interesting. One apparent roadblock to simulating a complex Stern-Gerlach setup is that we only have access to measurements in the “computational basis.” That is, we can only measure spin projection along the z axis. In terms of our simulated spins, ‘0’ refers to a measurement of +\frac{\hbar}{2} for \hat{S}^{z}, while ‘1’ represents a measurement of - \frac{\hbar}{2}. That seems pretty limiting. So we have to get clever. The trick I employ is explained incredibly well in this American Journal of Physics paper by Brody and Gruzman. Say you would like to measure spin along the axis \hat{n}(\theta,\phi). If you could somehow rotate your coordinate axes by \theta about the y axis and then \phi about the (original) z axis, your new z axis is aligned with \hat{n}. So if you perform the inverse operation, you’ll line up the \hat{n} direction with the \hat{z} axis. What is now a measurement of spin along the z direction in the rotated system is equivalent to a measurement of spin along the \hat{n} in the original system. Problem solved!

If we wish to measure the spin projection along some direction \hat{n}, we can rotate the system so that a measurement of the rotated state in the computational basis is equivalent to a measurement of the actual state in the desired basis.

Students are shown that “rotation gates” exist which can perform exactly such a rotation by a specified angle about a specified axis. As a simple example, we can measure \hat{S}^{x} on the state \left|+\right\rangle by simply rotating the system by \frac{-\pi}{2} about the y axis. I’ll drop a friendly reminder that in my course notation, \left|+\right\rangle refers to the state satisfying \hat{S}^{z}\left|+\right\rangle = \frac{\hbar}{2}\left|+\right\rangle. In quantum computing literature, this is the qubit state \left|0\right\rangle. From this point on, I’ll stop emphasizing that notational difference and exclusively work in my course notation.

Students know from the SPINS program that measuring \hat{S}^{x} on a beam of particles which just returned + \frac{\hbar}{2} from a measurement of \hat{S}^{z} will show an equal number of “up” and “down” spins. Here they find a similar distribution on the simulator and (up to errors, at least) on an actual quantum computer.

Results of measuring \hat{S}^{x} on the state \left|+\right\rangle (\left|0\right\rangle in quantum computing conventions) using QASM simulator and quantum hardware (ibmq_quito v1.0.18, one of the IBM Quantum Falcon Processors)

At this point, I introduce the general \hat{U} gate as a means for constructing an arbitrary initial state \left|\psi\right\rangle = \cos\frac{\theta}{2}\left|+\right\rangle + e^{i\phi}\sin\frac{\theta}{2}\left|-\right\rangle. Students’ final task is to measure the expectation values \left\langle\hat{S}^{\alpha}\right\rangle for \alpha = x,y,z on the state:

\displaystyle \left|+\right\rangle_{y} = \frac{1}{\sqrt{2}}\left(\left|+\right\rangle + i\left|-\right\rangle\right)

The general \hat{U}(\theta,\phi,\lambda) gate is given by

\displaystyle \hat{U}(\theta,\phi,\lambda) = \left(\begin{array}{cc}\cos\frac{\theta}{2} & -e^{i\lambda}\sin\frac{\theta}{2} \\ e^{i\phi}\sin\frac{\theta}{2} & e^{-i(\lambda + \phi)}\cos\frac{\theta}{2}\end{array}\right)

Now once students string together circuits to (a) generate this state and (b) measure one of the three spin operators, they have to turn the resulting counts into spin expectation values. At the end of the day, these simulations return a set of counts. I think it’s a valuable experience for students to work with these raw counts and compute experimental values for quantities which can be computed theoretically. Also knowing that we’re going to talk about the Heisenberg Uncertainty Principle in the coming days, it’s crucial that students also quantify statistical uncertainty for these results. The expectation value is a simple average. From the counts, students obtain N_{+} and N_{-} as the number of “up” and “down” measurements, respectively. Then (supposing we measured \hat{S}^{x})

\displaystyle \left\langle \hat{S}^{x}\right\rangle = \frac{N_{+}\left(+\frac{\hbar}{2}\right) + N_{-}\left(-\frac{\hbar}{2}\right)}{N_{+} + N_{-}} = \frac{\hbar}{2}\frac{N_{+}-N_{-}}{N_{+} + N_{-}}

A crude measure of statistical uncertainty in the estimate of this average is provided by the variance via \delta S^{x} = \sigma/\sqrt{N_{+}+N_{-}} where

\displaystyle \sigma^{2} = \frac{1}{\sqrt{N_{+}+N_{-}-1}}\left(N_{+}\left(\frac{\hbar}{2}-\left\langle \hat{S}^{x}\right\rangle\right)^{2} + N_{-}\left(-\frac{\hbar}{2}-\left\langle \hat{S}^{x}\right\rangle\right)^{2}\right)

I think this is an interesting point, because \sigma is the relevant quantity for the uncertainty principle, but \sigma/\sqrt{N} quantifies our uncertainty in this experimental estimate of the average. We’ll return to examining \sigma in the context of the uncertainty principle later. Also, because we aren’t monsters, we set \hbar = 1. Now students are able to compute spin expectation values with an estimate in experimental uncertainty:

Results for spin expectation values (\hbar = 1)
from ibqm_casablanca v1.2.30, one of the IBM Quantum Falcon Processors.

These can be compared to theoretical predictions \left\langle\hat{S}^{x}\right\rangle = \left\langle\hat{S}^{z}\right\rangle = 0 and \left\langle \hat{S}^{y}\right\rangle = \frac{1}{2} (up to the factor of \hbar). It’s worth keeping in mind that these statistical uncertainty estimates (a) are not hard limits and (b) only capture the statistical uncertainty associated with a finite sample size. In other words, they just give a rough ballpark for some kind of confidence interval and they don’t reflect systematic errors which might arise due to the imperfect quantum hardware. Admittedly, I think this kind of discussion runs the risk of obscuring the physics we’re trying to simulate. But at the same time, it’s important for students to think about how this imperfect hardware might lead to measurement error. At the end of the day, students find results that roughly agree with theoretical predictions, even if we can’t go as far as establishing firm uncertainty ranges which perfectly enclose the theoretical predictions.

Closing thoughts

By the end of this lab sessions, students are able to initialize arbitrary spin states \left|\psi\right\rangle, measure spin along an arbitrary axis, compute expectation values and associated statistical uncertainty that can be compared to theoretical predictions. I should emphasize that these tasks could also be simulated with the SPINS program or with a from-scratch script employing a random number generator. But what’s really cool here is that students are making legitimate measurements using real quantum hardware. There is no black box with a pseudo-random number generator used to produce these counts–it’s actual quantum mechanical behavior. In the coming weeks, we’ll set up some Stern-Gerlach protocols, investigate entanglement, and simulate time evolution.

References

I acknowledge the use of IBM Quantum services for this work. The views expressed are those of the author, and do not reflect the official policy or position of IBM or the IBM Quantum team. Additionally, I acknowledge the access to advanced services provided by the IBM Quantum Educators Program.

3 thoughts on “IBM Quantum/Qiskit in QM Part I: Single Spins”

  1. Pingback: IBM Quantum/Qiskit in QM Part II: Stern-Gerlach experiment – THEORETICALLY PHYSICS
  2. Pingback: IBM Quantum/Qiskit in QM Part III: Time evolution – THEORETICALLY PHYSICS
  3. Pingback: Foundational quantum experiments for the masses – THEORETICALLY PHYSICS

Leave a comment